IMU 101

What is IMU?

• IMU ＝ inertia measurement unit
• 3-axis accelerometer＋3-axis gyroscopes

source: https://www.ceva-dsp.com/ourblog/what-is-an-imu-sensor/

為什麼需要濾波？

加速度計會產生高頻振蕩的噪音訊號，又陀螺儀是將角速度對時間積分產生角度，故易產生誤差。

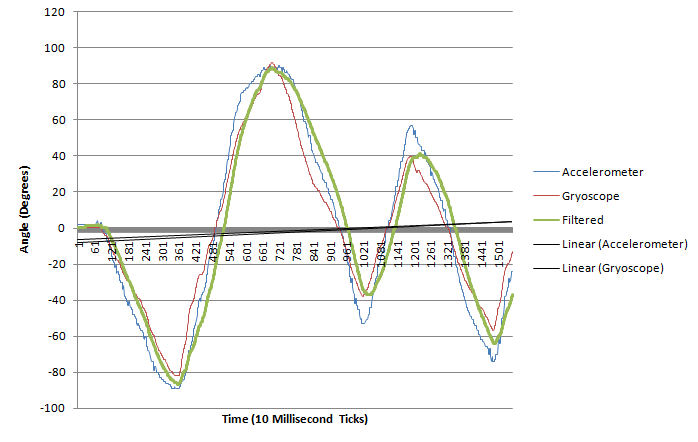
source: https://stackoverflow.com/questions/1586658/combine-gyroscope-and-accelerometer-data

互補濾波

Complementary filter

• 加速度計計算瞬時傾角誤差比較大
• 陀螺儀積分結果易受長時間影響

定時對加速度採樣的角度取平均值 + 短時間內採用陀螺儀得到的角度

加速度計要濾掉高頻訊號，陀螺儀要濾掉低頻訊號

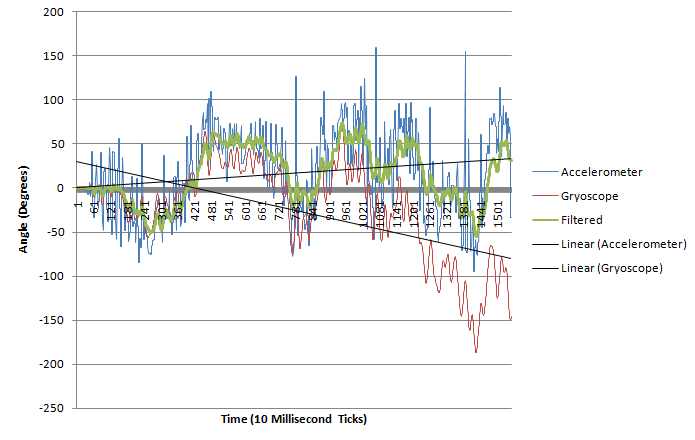
https://stackoverflow.com/questions/1586658/combine-gyroscope-and-accelerometer-data

$$
\text{angle’} = \alpha(\text{angle} + \text{gyro} \times dt) + (1-\alpha)\times(X_a)
$$

• \(\text{gyro}\) 為陀螺儀值(角速度)， \(dt\) 為計算週期
• \(X_A\) 為加速度數據換算後的角度值
• \(\alpha = 0.98\)

卡爾曼濾波

Kalman filter

• 線性
• 純時域
• 高斯雜訊

基本模型-真實狀態

$$
\displaylines{
x_k = Fx_{k-1}+Bu_k+w_k \\
w_k \sim N(0,\ Q_k)
}
$$

• \(x_k\) : \(k\) 時刻狀態
• \(F\) : 狀態變換矩陣
• \(u_k\) : 控制向量
• \(B\) : 控制輸入模型
• \(w_k\) : 過程雜訊
• \(Q_k\) : \(w_k\) 的共變異數矩陣

基本模型-觀測

$$
\displaylines{
z_k = Hx_k + v_k \\
v_k \sim N(0, R_k)
}
$$

• \(z_k\) : \(k\) 時刻測量到的狀態
• \(H\) : 觀測模型
• \(v_k\) : 觀測誤差
• \(R_k\) : \(v_k\) 的共變異數矩陣

預測

$$
\displaylines{
\hat{x}_ k^{-} = F\hat{x}_{k-1}+B\dot{\theta}_k \\
}
$$

• \(F=
  \begin{bmatrix}
  1 & -\Delta t \\
  0 & 1
  \end{bmatrix} \
  \hat{x}_k =
  \begin{bmatrix}
  \theta \\
  \dot{\theta}_b
  \end{bmatrix}_k \
  B=
  \begin{bmatrix}
  \Delta t \\
  0
  \end{bmatrix}\)
• \(P_k\) : \(x_k\) 的誤差共變異數矩陣
  • \(P_k = E[(x_k - E[x_k])(x_k - E[x_k])^T]\)
  • \(cov(AX+B,\ AX+B) = var(AX+B)\ = A\ var(X)\ A^T\)

修正

$$
\displaylines{
K_k = P_k^-H^T(HP^-_kH^T+R)^{-1} \\
\hat{x}_k = \hat{x}^-_k + K_k(z_k-H\hat{x}_k^-) \\
P_k = (I-K_kH)P^-_k
}
$$

• \(K_k\) : 卡爾曼增益 (最小化\(P_k\))
• \(H =
  \begin{bmatrix}
  1 & 0
  \end{bmatrix}\)

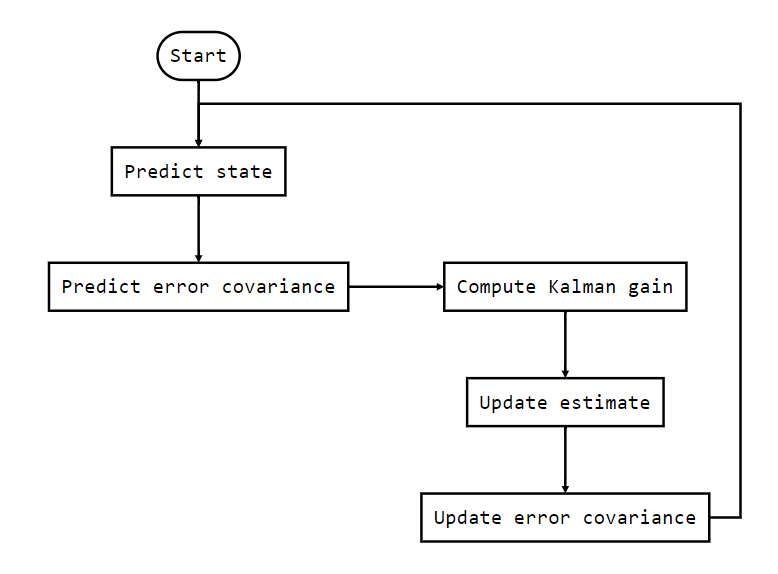
實作

裝置&流程

測試結果 Part 1

測試結果 Part 2

Pitch	Row

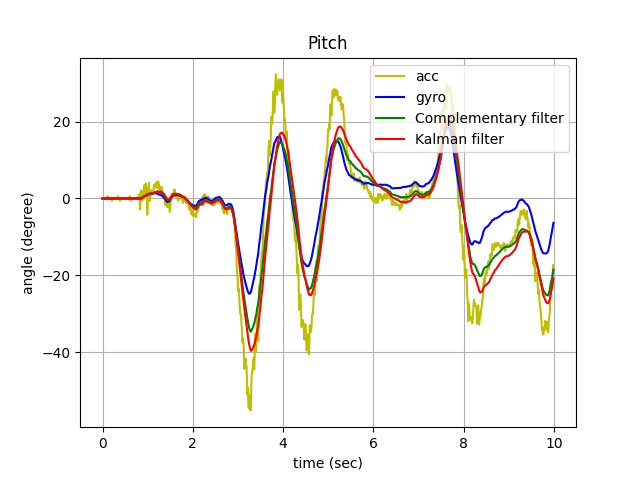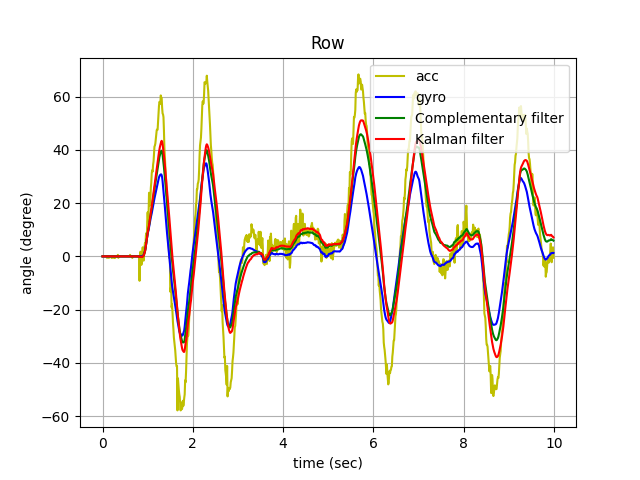Reference